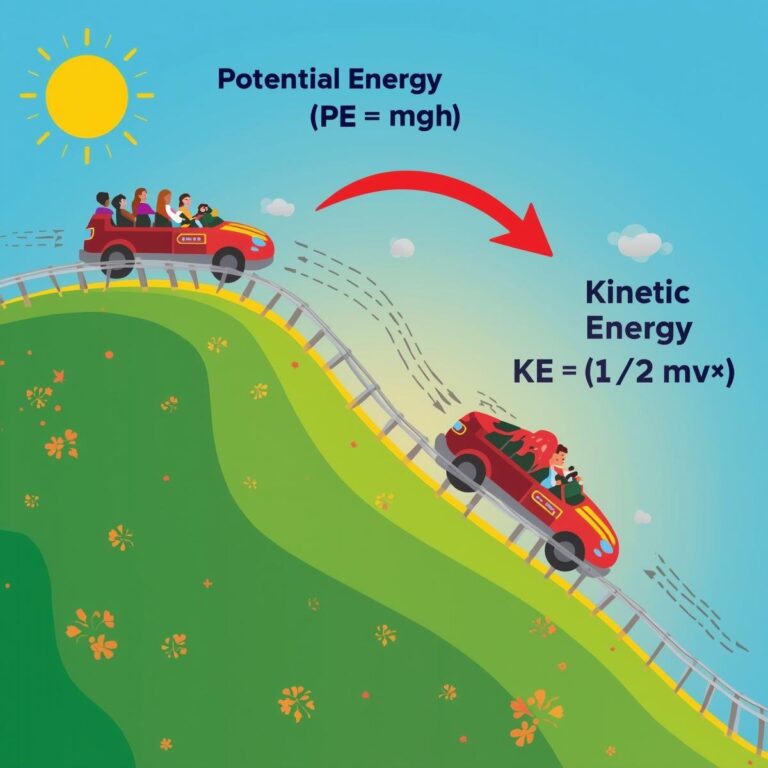
Electric Charge
Definition:
Electric charge is a fundamental property of matter that causes it to experience a force when placed in an electric or magnetic field. There are two types of electric charges: positive and negative. Like charges repel each other, while unlike charges attract.
Unit:
The SI unit of electric charge is the coulomb (C).
Example:
A glass rod rubbed with silk acquires a positive charge, while the silk becomes negatively charged.
Quantization of Charge:
Charge exists in discrete packets called quanta. The smallest unit of charge is the charge of an electron ((e)), where
( e = 1.6 \times 10^{-19} ) C.
Any charge (q) can be written as ( q = n \times e ), where ( n ) is an integer.
Electric Field
Definition:
The electric field at a point is the force experienced by a unit positive charge placed at that point. It is a vector quantity.
Mathematical Expression:
[ \vec{E} = \frac{\vec{F}}{q_0} ]
where ( \vec{E} ) is the electric field, ( \vec{F} ) is the force experienced, and ( q_0 ) is the test charge.
Unit:
The SI unit of electric field is newton per coulomb (N/C) or volt per meter (V/m).
Electric Field Due to a Point Charge
[ E = \frac{1}{4\pi\epsilon_0} \frac{q}{r^2} ]
where
- ( E ) = electric field at distance ( r ) from charge ( q )
- ( \epsilon_0 ) = permittivity of free space (( 8.85 \times 10^{-12} ) C(^2)/N·m(^2))
- ( q ) = point charge
- ( r ) = distance from the charge
Direction:
The electric field due to a positive charge is radially outward, and for a negative charge, it is radially inward.
Example:
Calculate the electric field at a point 0.2 m away from a charge of ( 5 \times 10^{-6} ) C.
[ E = \frac{1}{4\pi\epsilon_0} \frac{q}{r^2} = 9 \times 10^9 \times \frac{5 \times 10^{-6}}{(0.2)^2} ] [ E = 9 \times 10^9 \times \frac{5 \times 10^{-6}}{0.04} = 9 \times 10^9 \times 1.25 \times 10^{-4} = 1.125 \times 10^6 \text{ N/C} ]
Superposition Principle
The net electric field at a point due to multiple charges is the vector sum of the electric fields due to individual charges.
[ \vec{E}_{\text{net}} = \vec{E}_1 + \vec{E}_2 + \vec{E}_3 + \ldots ]
Key Formulas
- Coulomb’s Law:
[ F = \frac{1}{4\pi\epsilon_0} \frac{|q_1 q_2|}{r^2} ] - Electric Field:
[ \vec{E} = \frac{\vec{F}}{q_0} ] - Electric Field due to Point Charge:
[ E = \frac{1}{4\pi\epsilon_0} \frac{q}{r^2} ] - Quantization of Charge:
[ q = n \times e ]
Summary Table
| Concept | Formula/Definition | Unit |
|---|---|---|
| Electric Charge | ( q = n \times e ) | Coulomb (C) |
| Electric Field | ( \vec{E} = \frac{\vec{F}}{q_0} ) | N/C or V/m |
| Point Charge Field | ( E = \frac{1}{4\pi\epsilon_0} \frac{q}{r^2} ) | N/C |
electric charge