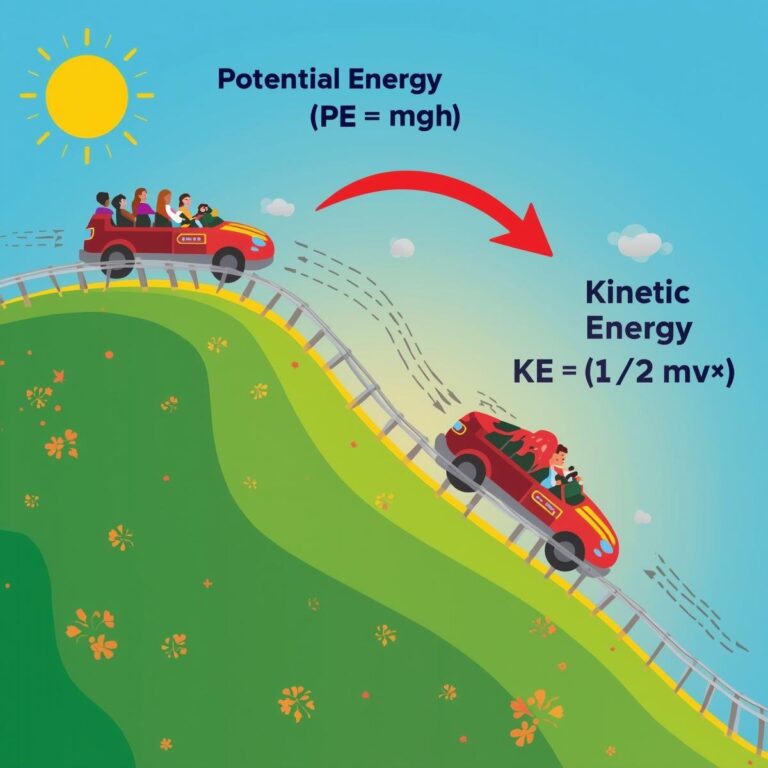
Distance
The total length traveled by any object in a any interval of time is called distance.
Dimensional Formula
x = s
D.F. = [L] also waiting as
= [M⁰L¹T⁰]
S.I. Unit = m(meter)
It is a scalar quality.
It is always positive.
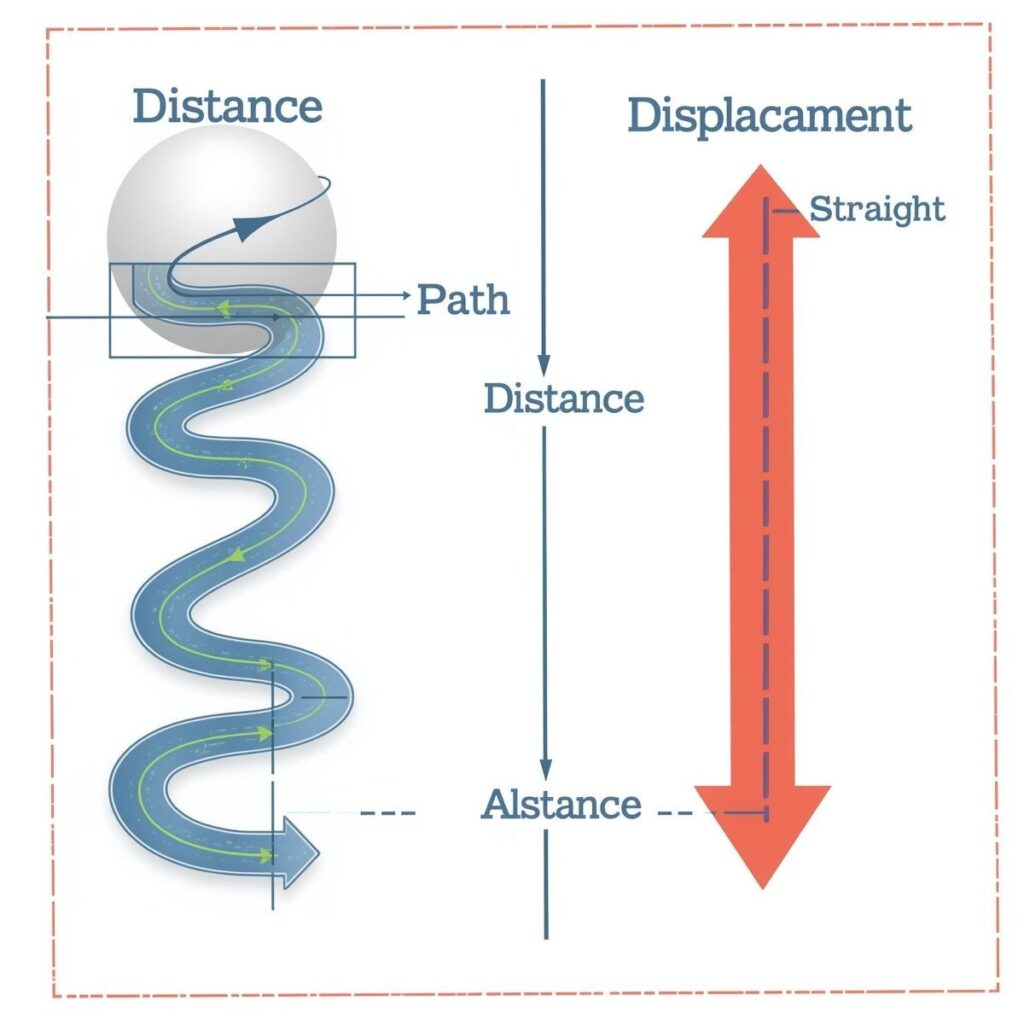
Displacement
The total distance traveled by the object in specific direction is called displacement.
or
The difference of final and initial distance is known as displacement.
It is denoted by ∆x = x2-x1
Dimensional Formula
D.F. = [L] also waiting as
= [M⁰L¹T⁰]
S.I. Unit = m(meter)
It is a Vector quality.
It is may be positive, negative or even zero.
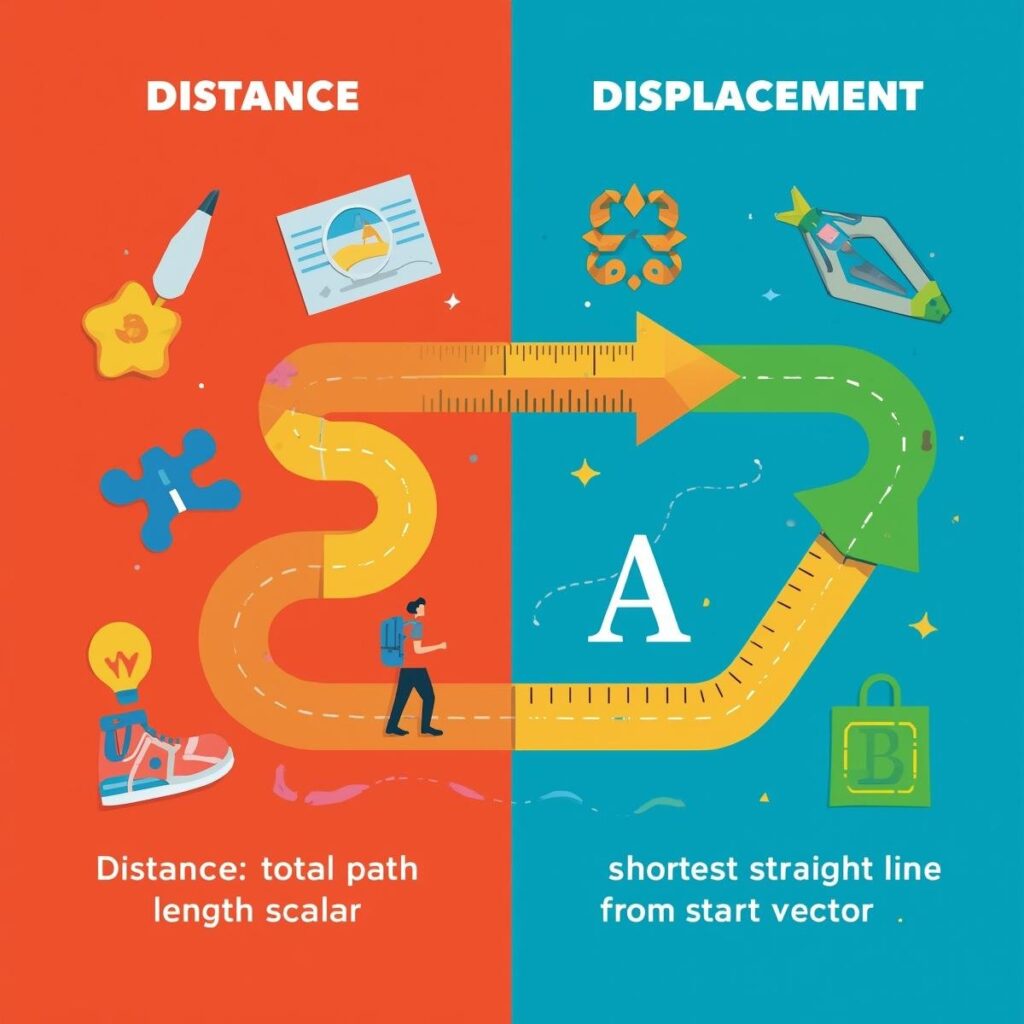
Distance:
- Distance is the total length of the actual path traveled by an object, regardless of direction.
- It is a scalar quantity (has only magnitude, no direction).
- The SI unit of distance is meter (m).
- Distance can never be negative or zero (unless the object hasn’t moved).
Example:
If you walk 3 meters east and then 4 meters west, the total distance traveled is 3 m + 4 m = 7 m.
Displacement:
- Displacement is the shortest straight-line distance from the initial position to the final position of an object, along with the direction.
- It is a vector quantity (has both magnitude and direction).
- The SI unit of displacement is also meter (m).
- Displacement can be positive, negative, or zero.
Example:
If you walk 3 meters east and then 4 meters west, your displacement is 3 m (east) + (–4 m) (west) = –1 m (west). The magnitude is 1 m, direction is west.
Key Differences:
- Distance measures the path length; displacement measures the shortest straight-line distance.
- Distance is scalar; displacement is vector.
- Distance is always positive; displacement can be zero, positive, or negative.
Formulas for Distance and Displacement
Distance:
- There is no fixed formula for distance, as it depends on the actual path taken.
- For straight-line motion:
Distance = Total path length traveled
Displacement:
- For straight-line motion:
Displacement = Final position – Initial position - If the motion is along a straight line (say, on the x-axis):
Displacement (Δx) = x₂ – x₁
where x₂ = final position, x₁ = initial position
For motion in two dimensions (using coordinates):
- If an object moves from point A (x₁, y₁) to point B (x₂, y₂):
Displacement = √[(x₂ – x₁)² + (y₂ – y₁)²]