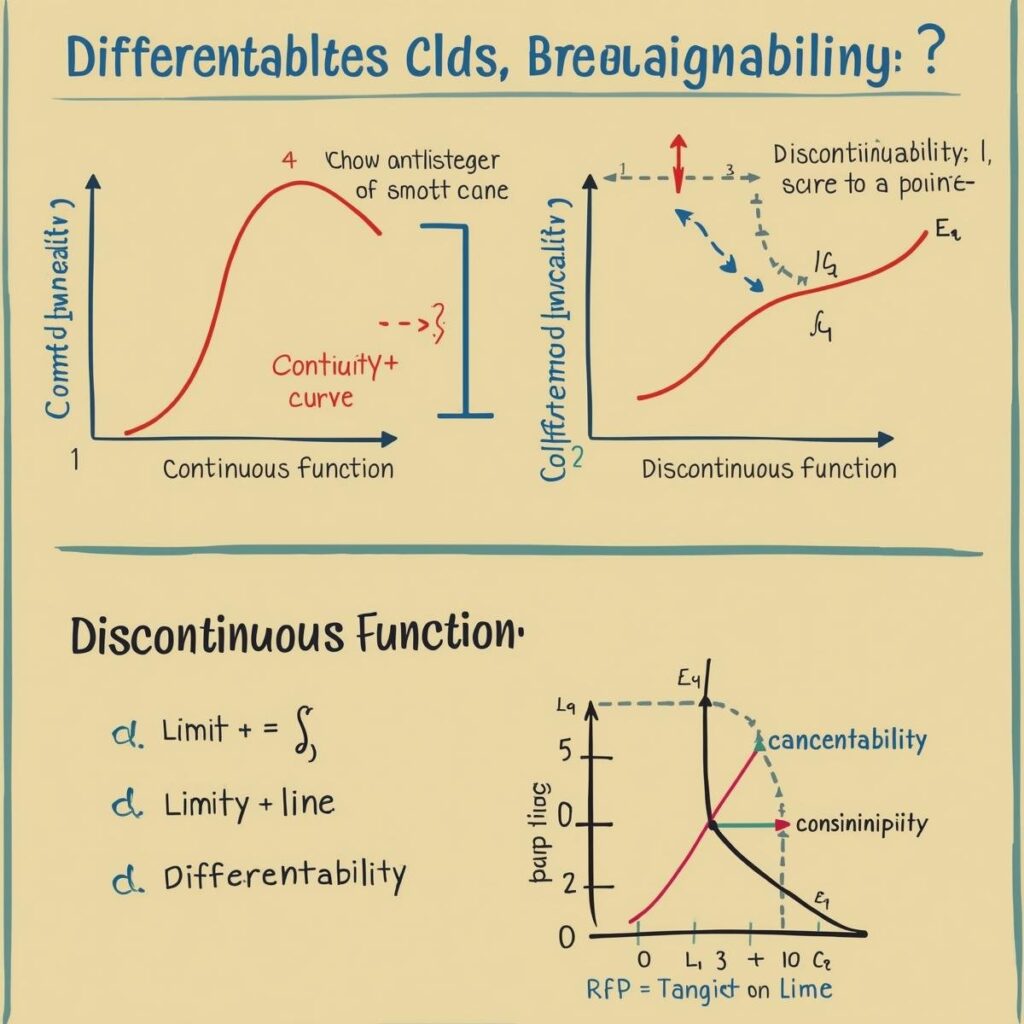
Continuity
Definition
A function f(x) is said to be continuous at a point x = a if
[\lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) = f(a)]
That is, the left-hand limit, right-hand limit, and the value of the function at x = a are all equal.
A function is continuous in an interval if it is continuous at every point in that interval.
Example
Let (f(x) = 3x + 2).
Check continuity at x = 1:
[\lim_{x \to 1} f(x) = 3(1) + 2 = 5]
(f(1) = 5)
Since the limit and the value are equal, f(x) is continuous at x = 1.
Differentiability
Definition
A function f(x) is differentiable at x = a if the derivative exists at that point, i.e.,
[\lim_{h \to 0} \frac{f(a+h) – f(a)}{h}]
exists and is finite.
A function is differentiable in an interval if it is differentiable at every point in that interval.
Note: Every differentiable function is continuous, but every continuous function may not be differentiable.
Example
Let (f(x) = x^2).
The derivative at x = 2:
[\frac{d}{dx} (x^2) = 2x]
At x = 2, derivative = 2 × 2 = 4.
So, f(x) is differentiable at x = 2.
Formulas
Continuity
- For polynomial, rational, trigonometric, exponential, and logarithmic functions, continuity holds in their domains.
- For piecewise functions, check continuity at the points where the definition changes.
Differentiability
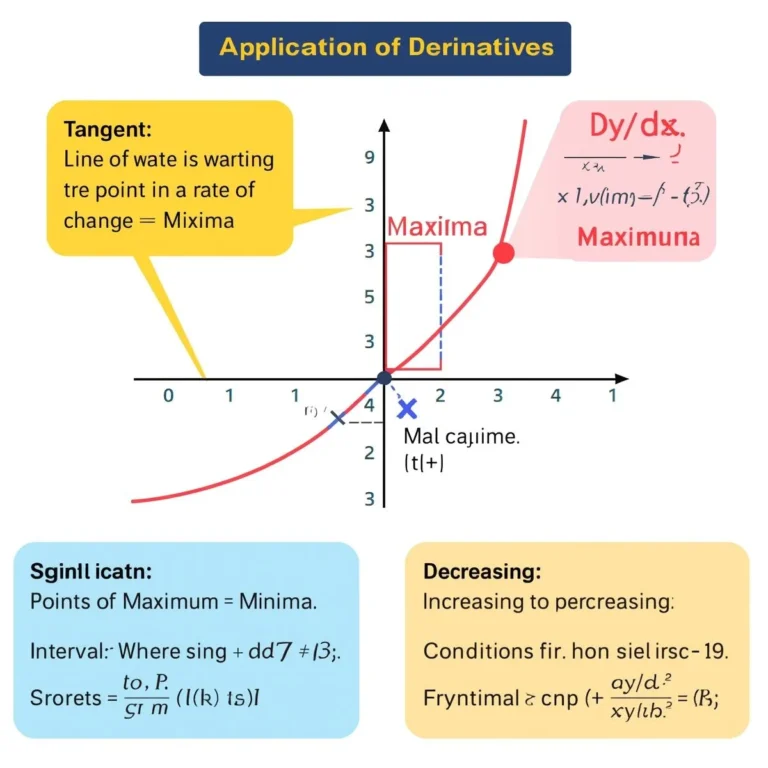
- Derivative of sum: (\frac{d}{dx}[f(x) + g(x)] = f'(x) + g'(x))
- Derivative of product: (\frac{d}{dx}[f(x)g(x)] = f'(x)g(x) + f(x)g'(x))
- Derivative of quotient: (\frac{d}{dx}\left[\frac{f(x)}{g(x)}\right] = \frac{f'(x)g(x) – f(x)g'(x)}{[g(x)]^2})
- Chain rule: (\frac{d}{dx}f(g(x)) = f'(g(x)) \cdot g'(x))
Important Points
- If a function is differentiable at a point, it is also continuous at that point.
- If a function is not continuous at a point, it is not differentiable there.
Summary Table
| Concept | Definition | Test/Formula | Example |
|---|---|---|---|
| Continuity | No break/jump at a point | LHL = RHL = f(a) | f(x) = 3x+2 at x=1 |
| Differentiability | Derivative exists at a point | (\lim_{h \to 0} \frac{f(a+h)-f(a)}{h}) | f(x) = x² at x=2 |
Example: Continuity and Differentiability at a Point
Let
(f(x) = \begin{cases} x^2, & x < 1 \ 2x-1, & x \geq 1 \end{cases})
- Continuity at x = 1:
(\lim_{x \to 1^-} f(x) = (1)^2 = 1)
(\lim_{x \to 1^+} f(x) = 2(1) – 1 = 1)
(f(1) = 2(1) – 1 = 1)
All equal ⇒ f(x) is continuous at x = 1. - Differentiability at x = 1:
Left derivative: (\frac{d}{dx}(x^2) = 2x), at x = 1: 2
Right derivative: (\frac{d}{dx}(2x-1) = 2), at x = 1: 2
Both derivatives are equal ⇒ f(x) is differentiable at x = 1.