Definition
The application of derivatives refers to the use of derivatives to solve various types of real-life and mathematical problems, such as finding the rate of change, maxima and minima, increasing and decreasing functions, tangents and normals, and approximations.
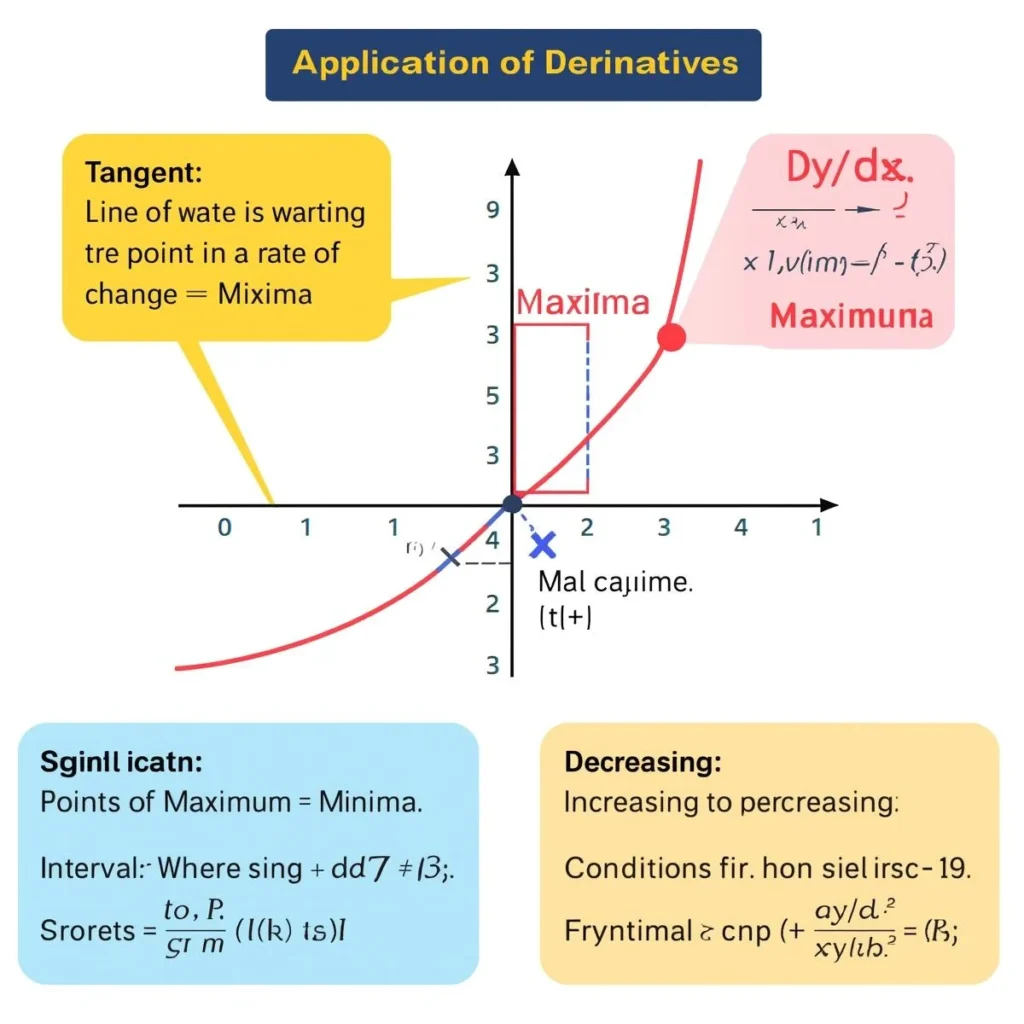
Key Applications
1. Rate of Change
The derivative of a function represents the rate at which one quantity changes with respect to another.
Formula:
If ( y = f(x) ), then the rate of change of y with respect to x is ( \frac{dy}{dx} ).
Example:
If the radius of a circle increases at a rate of 2 cm/s, find the rate at which the area increases when the radius is 5 cm.
Area, ( A = \pi r^2 )
( \frac{dA}{dt} = 2\pi r \frac{dr}{dt} = 2\pi \times 5 \times 2 = 20\pi ) cm²/s
2. Increasing and Decreasing Functions
A function is increasing where its derivative is positive and decreasing where its derivative is negative.
Test:
- If ( f'(x) > 0 ) in an interval, f(x) is increasing there.
- If ( f'(x) < 0 ) in an interval, f(x) is decreasing there.
Example:
For ( f(x) = x^2 ), ( f'(x) = 2x ).
- Increasing for ( x > 0 )
- Decreasing for ( x < 0 )
3. Maxima and Minima
Derivatives help find local maximum and minimum values of a function.
Test:
- If ( f'(a) = 0 ) and ( f”(a) < 0 ), f(x) has a local maximum at x = a.
- If ( f'(a) = 0 ) and ( f”(a) > 0 ), f(x) has a local minimum at x = a.
Example:
Find the maximum or minimum of ( f(x) = x^2 – 4x + 3 ).
( f'(x) = 2x – 4 )
Set ( f'(x) = 0 ) ⇒ ( x = 2 )
( f”(x) = 2 > 0 ), so minimum at ( x = 2 ).
Minimum value: ( f(2) = 2^2 – 4 \times 2 + 3 = 4 – 8 + 3 = -1 )
4. Tangents and Normals
The derivative at a point gives the slope of the tangent to the curve at that point.
Formulas:
- Slope of tangent at ( (x_1, y_1) ): ( m = f'(x_1) )
- Equation of tangent: ( y – y_1 = f'(x_1)(x – x_1) )
- Equation of normal: ( y – y_1 = -\frac{1}{f'(x_1)}(x – x_1) )
Example:
Find the equation of the tangent to ( y = x^2 ) at ( x = 1 ).
( f'(x) = 2x ), at ( x = 1 ), ( f'(1) = 2 )
Point: (1, 1)
Equation: ( y – 1 = 2(x – 1) ) ⇒ ( y = 2x – 1 )
5. Approximations
Derivatives can be used to approximate small changes in a function.
Formula:
If ( y = f(x) ), then for small ( \Delta x ),
( \Delta y \approx f'(x) \Delta x )
Example:
If ( y = x^2 ), estimate the change in y when x changes from 2 to 2.01.
( f'(x) = 2x ), at ( x = 2 ), ( f'(2) = 4 )
( \Delta x = 0.01 )
( \Delta y \approx 4 \times 0.01 = 0.04 )
Summary Table
| Application | Formula/Method | Example |
|---|---|---|
| Rate of Change | ( \frac{dy}{dx} ) | Area of circle increasing |
| Increasing/Decreasing | ( f'(x) > 0 ) or ( < 0 ) | ( f(x) = x^2 ) |
| Maxima/Minima | ( f'(a) = 0, f”(a) < 0 ) or ( > 0 ) | ( f(x) = x^2 – 4x + 3 ) |
| Tangents/Normals | Slope = ( f'(x_1) ) | Tangent to ( y = x^2 ) at ( x = 1 ) |
| Approximations | ( \Delta y \approx f'(x) \Delta x ) | ( y = x^2, x: 2 \to 2.01 ) |