Definition
Relation
A relation from a set A to a set B is a subset of the Cartesian product A × B. It describes how elements of one set are related to elements of another set.
Function
A function is a special type of relation in which every element of set A (domain) is associated with exactly one element of set B (codomain).
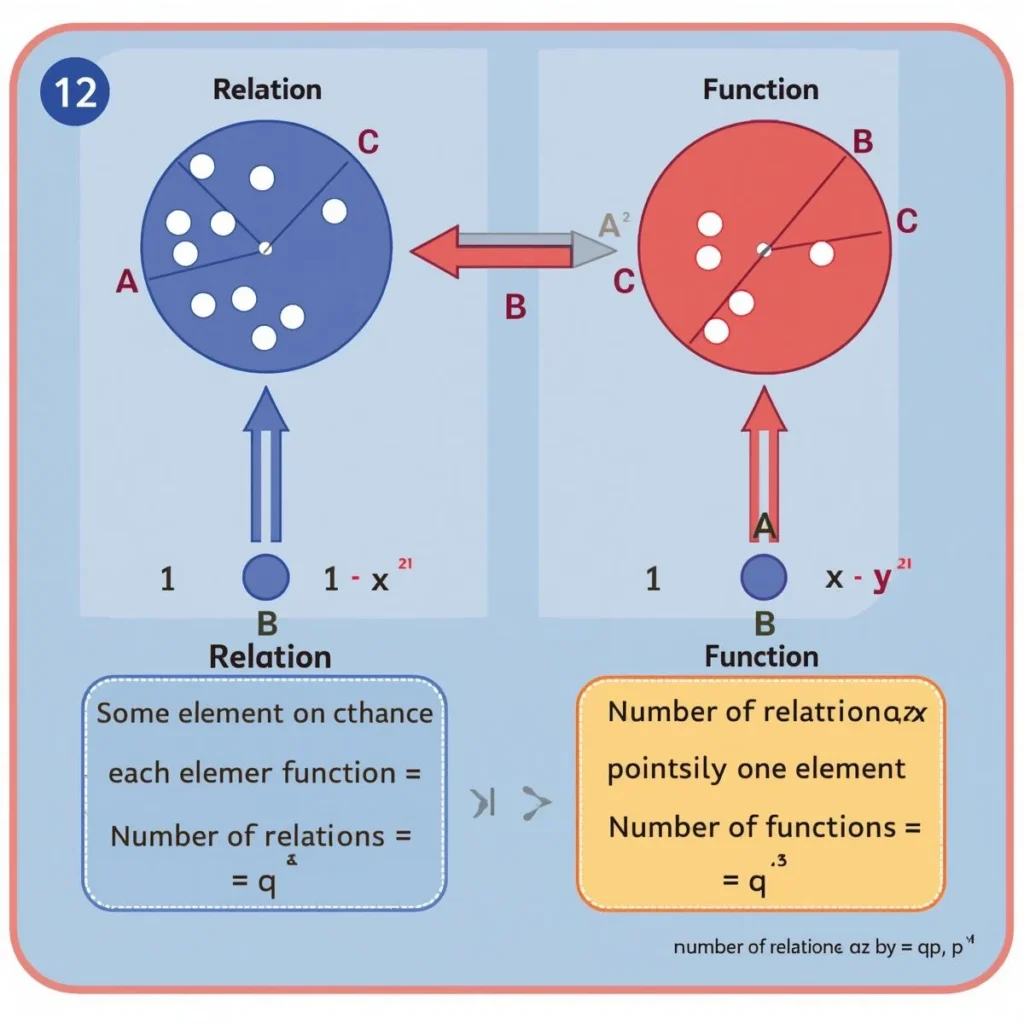
Formulas
- Cartesian Product:
If A and B are two sets, then
A × B = { (a, b) | a ∈ A, b ∈ B } - Number of Relations:
If n(A) = p and n(B) = q, then the number of relations from A to B is 2^(p×q). - Number of Functions:
If n(A) = p and n(B) = q, then the number of functions from A to B is q^p.
Example
Let A = {1, 2}, B = {x, y}
- Cartesian Product:
A × B = { (1, x), (1, y), (2, x), (2, y) } - Relation Example:
R = { (1, x), (2, y) } is a relation from A to B. - Function Example:
f: A → B defined by f(1) = x, f(2) = y is a function from A to B.
Types of Functions
- One-One (Injective): Each element of A maps to a unique element of B.
- Onto (Surjective): Every element of B is the image of at least one element of A.
- Bijective: Both one-one and onto.
Illustrative Image
Summary Table
| Concept | Description |
|---|---|
| Relation | Subset of A × B |
| Function | Relation with each element of A mapped to one element of B |
| Number of Relations | 2^(p×q) |
| Number of Functions | q^p |
| Example Relation | {(1, x), (2, y)} |
| Example Function | f(1) = x, f(2) = y |