Work-Energy Theorem (Class 11)

Definition

The work-energy theorem states that the net work done by all the forces acting on a particle is equal to the change in its kinetic energy. When work is done on an object, it results in a change in the object’s kinetic energy.

Formula

W_net = ΔKE = KE_final – KE_initial

Where:

W_net = net work done by all forces (Joule, J)
KE_final = final kinetic energy (J)
KE_initial = initial kinetic energy (J)
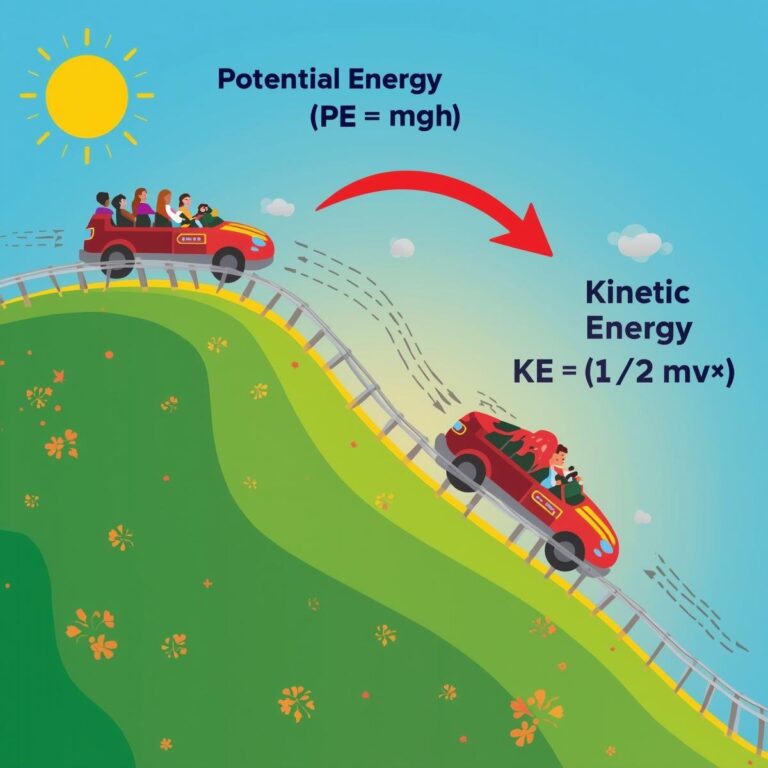
KE = (1/2)mv² (m = mass, v = velocity)

Derivation

Consider a particle of mass m moving in a straight line under the action of a net force F.

From Newton’s second law:
F = m·a

If the particle moves a small distance dx under this force, the work done dW is:
dW = F·dx

Since acceleration a = dv/dt, and velocity v = dx/dt,
a = dv/dt = (dv/dx)·(dx/dt) = v·dv/dx

So,
F = m·a = m·v·dv/dx

Therefore,
dW = F·dx = m·v·dv/dx·dx = m·v·dv

Integrate both sides from initial velocity u to final velocity v:
∫(from u to v) m·v·dv = ∫(from x₁ to x₂) dW

m ∫(from u to v) v·dv = W_net

m [ (1/2) v² ] (from u to v) = W_net

m [ (1/2) v² – (1/2) u² ] = W_net

W_net = (1/2) m v² – (1/2) m u²

W_net = KE_final – KE_initial

This proves the work-energy theorem.

Example

A ball of mass 2 kg is initially at rest. A force acts on it and accelerates it to a velocity of 5 m/s.

Initial velocity, u = 0
Final velocity, v = 5 m/s
Mass, m = 2 kg

Initial kinetic energy, KE_initial = (1/2) × 2 × (0)² = 0 J
Final kinetic energy, KE_final = (1/2) × 2 × (5)² = 25 J
Change in kinetic energy, ΔKE = 25 J – 0 J = 25 J

According to the work-energy theorem, the net work done on the ball is 25 J.

Key Points

The theorem applies to all types of forces (conservative and non-conservative).
If net work is positive, kinetic energy increases.
If net work is negative, kinetic energy decreases.

Illustrative Image

Summary Table

Aspect	Description
Definition	Net work done equals change in kinetic energy
Formula	W_net = KE_final – KE_initial
SI Unit	Joule (J)
Example	Ball accelerated from rest to 5 m/s: W_net = 25 J